梅涅劳斯 (Menelaus) 定理

8

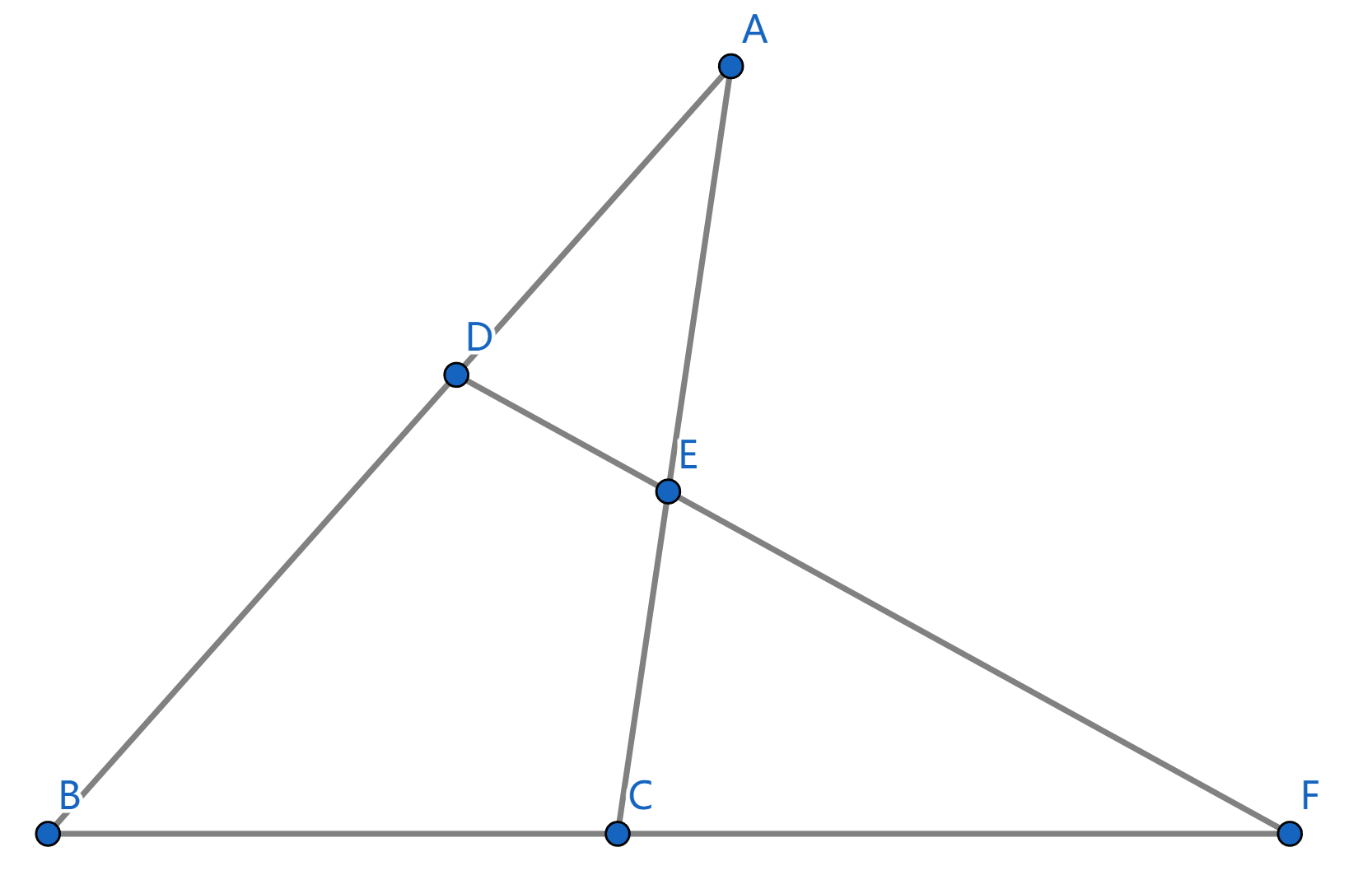
menelaus_1.png
点 D, E, F 分别是 \triangle ABC 三边 AB, AC, BC 所在直线上的点, 且 D, E, F 三点共线, 则有

\frac{AD}{DB} \cdot \frac{BF}{FC} \cdot \frac{CE}{EA} = 1.

证明

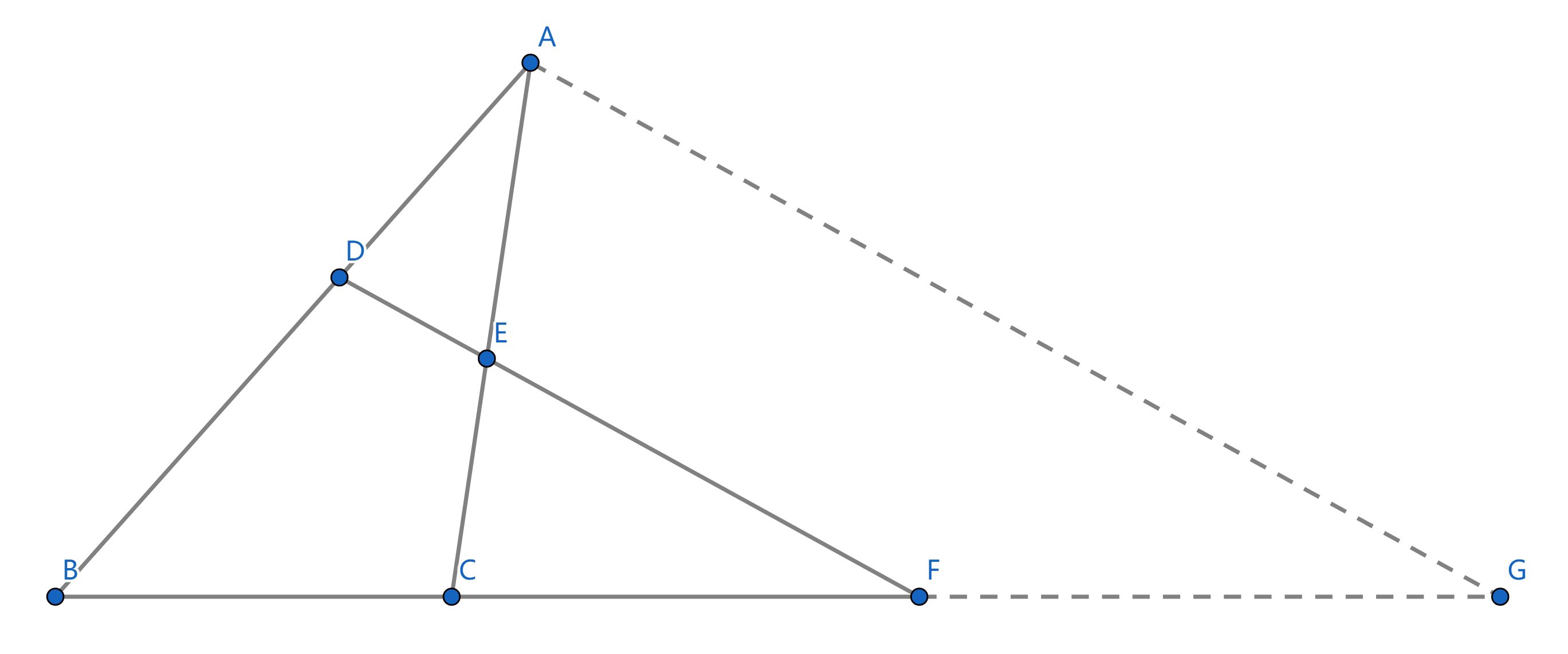
menelaus_2.png
过 A 作 DF 的平行线, 交 BC 所在直线于 G.

显然有

\frac{AD}{DB} = \frac{FG}{BF}, \frac{CE}{EA} = \frac{FC}{FG}

因此

\frac{AD}{DB} \cdot \frac{BF}{FC} \cdot \frac{CE}{EA} = \frac{FG}{BF} \cdot \frac{BF}{FC} \cdot \frac{FC}{FG} = 1.