斯特瓦尔特 (Stewart) 定理

16

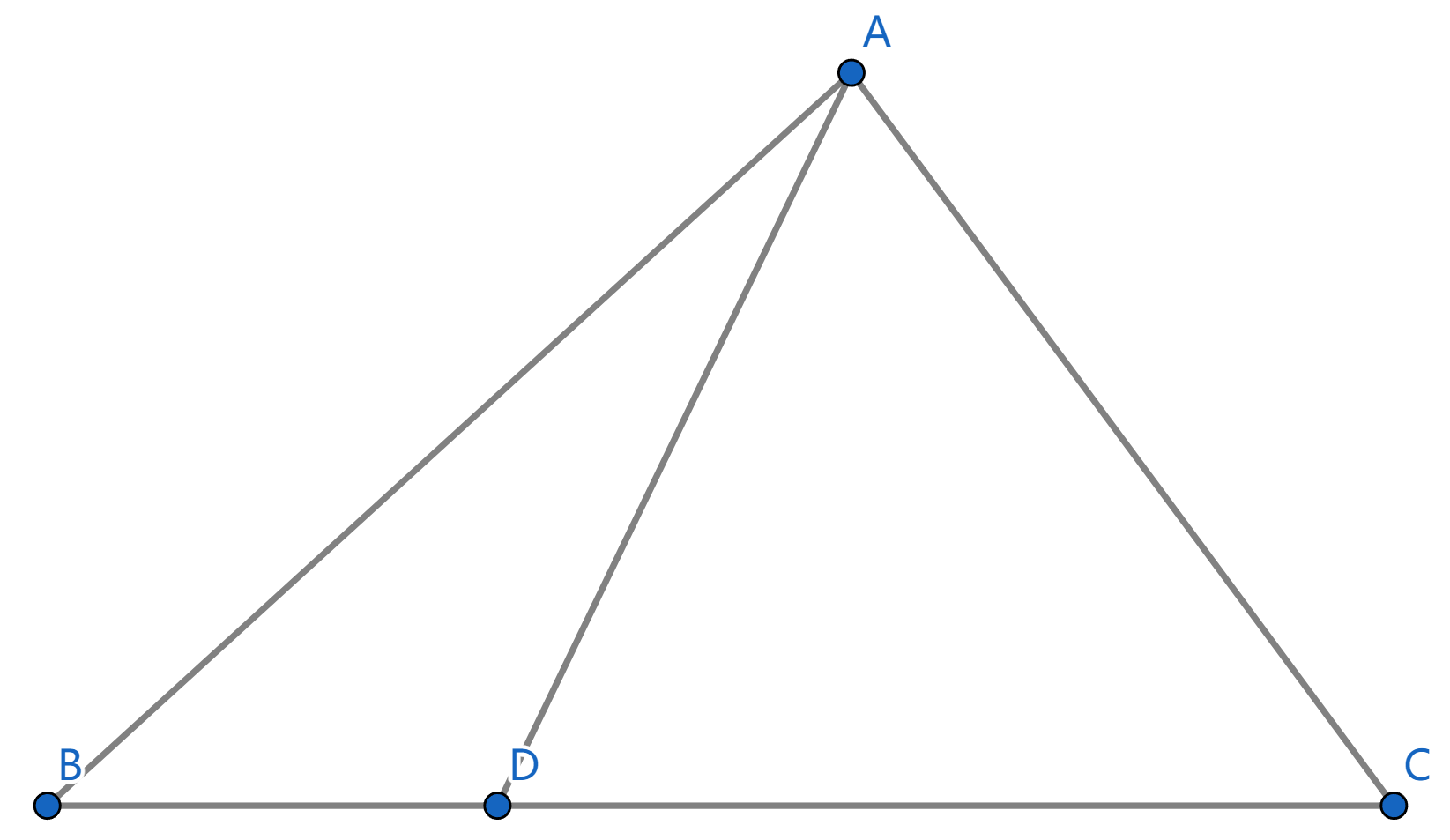
stewart_1.png
在 \triangle ABC 中, D 是边 BC 上异于 B, C 的一点, 连接 AD, 则有

AB^2 \cdot CD + AC^2 \cdot BD - AD^2 \cdot BC = BC \cdot CD \cdot BD.

证明

在 \triangle ABD 中, 由余弦定理得

AD^2 = AB^2 + BD^2 - 2AB \cdot BD \cdot \cos B

在 \triangle ABC 中, 由余弦定理得

\cos B = \frac{AB^2 + BC^2 - AC^2}{2AB \cdot BC}

因此

AD^2 = AB^2 + BD^2 - 2AB \cdot BD \cdot \frac{AB^2 + BC^2 - AC^2}{2AB \cdot BC}
\Rightarrow AD^2 \cdot BC = AB^2 \cdot BC + BD^2 \cdot BC - BD \cdot (AB^2 + BC^2 -AC^2)
\Rightarrow AB^2 \cdot CD + AC^2 \cdot BD - AD^2 \cdot BC = BC \cdot CD \cdot BD.